Na edição passada, a professora Franciele Fey escreveu sobre a Geometria Fractal e sobre a diferença entre a Geometria Euclidiana, nessa edição eu vou falar sobre a Geometria de Euclides, mais precisamente entre os objetos em três dimensões, os “sólidos”.
Os sólidos são objetos tridimensionais, formados pela união de figuras bidimensionais, calma eu explico. Juntando seis quadrados (figura de duas dimensões), podemos fazer um cubo (figura de três dimensões). É importante ressaltar a diferença entre esses dois conceitos.
Todos os sólidos são constituídos por três elementos básicos: Faces, Arestas e Vértices. As faces são a parte mais fácil de se visualizar, o cubo, por exemplo, tem seis faces. As arestas não são complicadas de se ver, toda intersecção entre duas faces faz uma aresta; de novo o cubo, tem 12 arestas. E os vértices é toda intersecção entre três ou mais faces; o cubo tem 8.
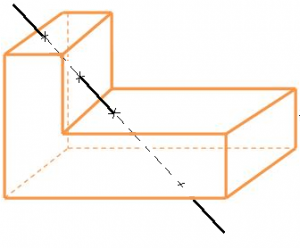Euler, um matemático suíço criou uma relação algébrica entre esses elementos dos sólidos. V-A+F=2, onde “V” é a quantidade de vértices, “A” é a quantidade de arestas e “F” a de faces. Essa relação vale para todos os sólidos convexos e para alguns não convexos. Lembrando que um sólido convexo é um que podemos passar uma reta por ele e ela entra de um lado e sai de outro; um sólido não convexo é o que podemos passar uma reta através dele de tal forma que ela entre de um lado, passe por uma parte fora do sólido e entre no sólido de novo e saia de outro lado. Na imagem uma melhor explicação desses sólidos não convexos.
Os sólidos platônicos são os mais comuns de se estudar, são eles o tetraedro, o hexaedro (cubo), o octaedro o dodecaedro e o icosaedro. Os nomes provêm da quantidade de faces que tem, “tetra” é quatro, “hexa” é seis, icosa” é vinte. São também, os mais fáceis de se construir.
Há também os sólidos de Arquimedes, de Catalan de Kepler-Poinsot, prismas, antiprismas, esferas, cilindros, pirâmides, bipirâmides…
Enquanto os sólidos de Platão têm todas as suas faces de um mesmo polígono (vê a diferença entre polígono e poliedro, bidimendional e tridimensional), os sólidos de Arquimedes têm suas faces compostas por mais de um tipo de polígono, mas ainda todos regulares.
Os sólidos de Catalan são os sólidos duais dos sólidos de Arquimedes, ou seja, de cada uma das faces do sólido é encostada por um vértice de um sólido dual dentro dele. Os de Catalan são os duais dos de Arquimedes e vice-versa, os de Platão têm seus duais entre eles mesmos.
No blog da Matemática Faccat (matematicafaccat.blogspot.com) tem a planificação de alguns sólidos para ser construído. Tenta fazer alguns!